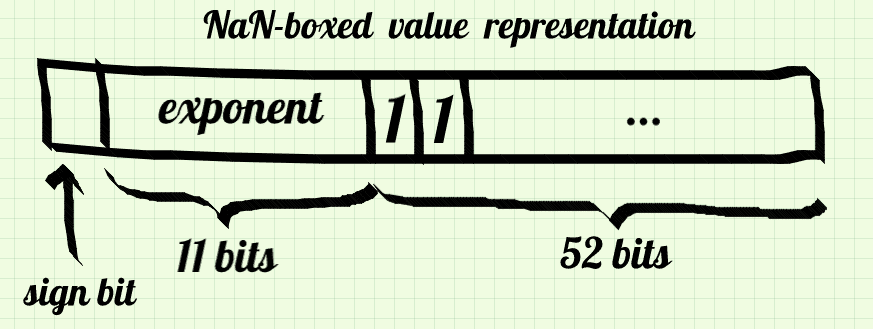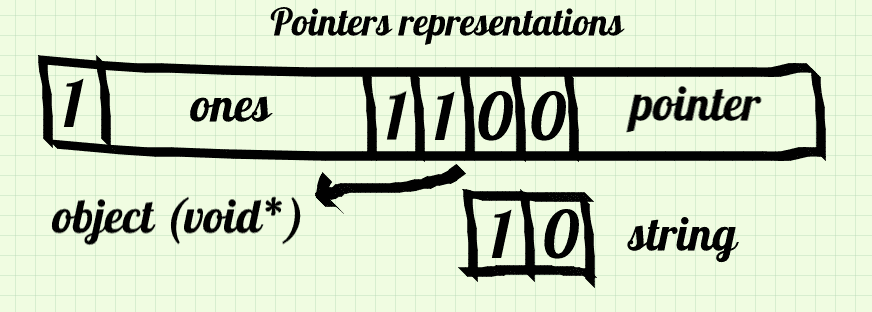NaN boxing or how to make the world dynamic

There are many programming languages that are dynamically typed, which means that you can reassign variables many times using completely different types of value. Let’s see this in JavaScript:

let a = "foo"; //It starts as a string
a = {bar: 1};  //Then it's an object
a = 123;       //And ends as a number

Some people criticize this style, some find it useful. No matter what group you belong to, doesn’t it seem interesting how this works? I will show you some solutions, but the most interesting will be the last one, so wait for it :)

General idea for this article

Let’s say we are implementing our own dynamically-typing language in C, like e.g. CPython. We need to invent a way of recognizing types of our values and storing different types of them. Of course, these processes should be as simple as possible and memory-efficient, so that our virtual machine can run blazingly fast.

For the sake of this article, we assume that our language supports six possible types:

1. 64-bit floating-point numbers,
2. 32-bit integers,
3. strings,
4. null,
5. booleans,
6. objects.

They create a wide spectrum of representations. Numbers can occupy 64 or 32 bits, null is just one special value and for booleans, we need two of them: true and false. Objects and strings have to be stored as pointers, as we do not know in advance their size. Moreover, the size of a pointer depends on the chip’s architecture. In most modern computers, they can have 32 or 64 bits.

How to pack all of them?

Very very bad approach

This might be the first solution that comes to mind. We define a struct with an enum tag, which tells what type the value holds now, and has all possible types listed.

typedef struct {
  enum {
    TYPE_DOUBLE,
    TYPE_INT,
    TYPE_STRING,
    TYPE_OBJECT,
    TYPE_BOOLEAN,
    TYPE_NULL
  } type;

  double as_double;
  int32_t as_int;
  char* as_string;
  void* as_object;
  char as_boolean; //There is no bool type in old C
} value;

Probably you have noticed that we do not have the as_null field. That is, of course, because null has only one possible value, so if we know it is null, there is no need to analyze its value further.

Setting different values here is pretty straightforward:

value foo;

//Let's set int
foo.type = TYPE_INT;
foo.as_int = 123;

//Now, boolean
foo.type = TYPE_BOOLEAN;
foo.as_boolean = 0; //This is false

//And pointer to string
foo.type = TYPE_STRING;
foo.as_string = "bar";

Testing types and reading values is also not a rocket-science:

switch(foo.type){
  case TYPE_DOUBLE:
    printf("%lf", foo.as_double);
    break;
  case TYPE_NULL:
    printf("null");
  case TYPE_STRING:
    printf("%s", foo.as_string);
    break;
  default:
    printf("It's something else");
}

It seems to work, doesn’t it? Everything is easy, we can store different values and even do not have to care about any C type size. Actually, we do not care about size at all.

And this is wrong.

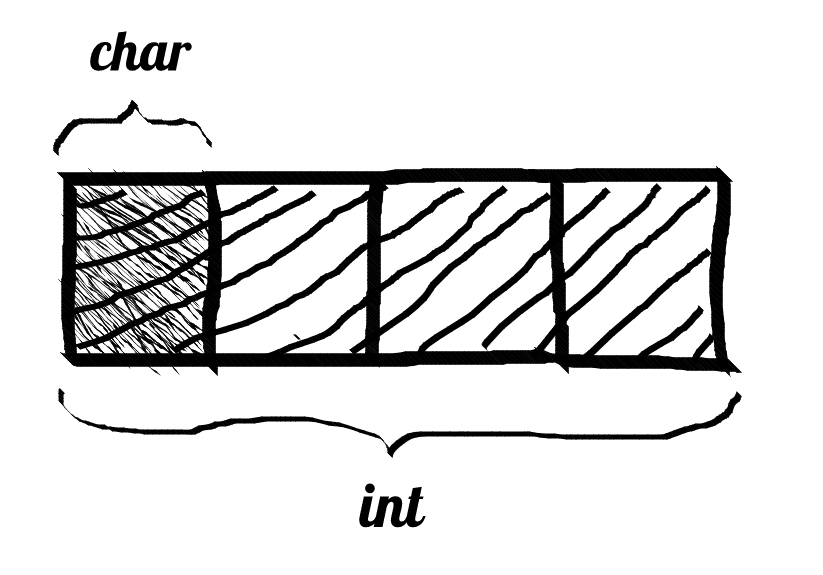
Let’s count how big is our value struct, assuming we are programming for some 64-bit systems.

1. enum type is probably the same size as int — typically 4 bytes
2. double as_double should have 64 bits — 8 bytes
3. int32_t as_int has 32 bits — 4 bytes
4. char* as_string is a pointer — 64 bits or 8 bytes
5. void* as_object the same — 8 bytes
6. char as_boolean is usually pretty small — 1 byte

The sum of these sizes gives us 33 bytes (or 264 bits). Well, we had better check our calculations:

printf("%d\n", sizeof(value));

On my computer, compiled with gcc, it displays 48. It is much more than our 33 bytes. Are our calculations so much wrong?

Padding

They are actually right in terms of additions. However, structs in C do not behave this way. The sum of ingredients does not have to be the overall size of a struct. This happens because of an effect called padding. The compilers are to blame for it. They can put some empty space inside of a struct or after it in order to make the overall size look better.

What does it mean better? Let’s do a little recap of how computers work closer to the metal.

When CPU wants to read something from memory, it has to read whole words — chunks of data of fixed size, usually like 64 or 32 bits. If our struct has such a good size, the CPU can read it pretty directly and fast. If not, like our 33-byte value struct with one dangling byte, CPU has to do some shifts in memory and it is harder to pack more of these structs in its registers.

Because of that, compilers put some empty bytes between our struct members or at the end of a struct in order to ensure that the overall size will be good enough for CPU. A compiler can also change the order of fields if this could improve the speed of reading them. This is also a reason why it is not a good idea to directly serialize structs as binary data — the same struct can look differently on different computers.

Let’s go back to our code

It seems like a compiler added 15 empty bytes somewhere in the struct, making it by almost 50% bigger just in vain (for us, for CPU it could be better). We could reduce the size to 32 bytes just by removing some fields and trying to move its function somewhere else. For example, we can get rid of as_boolean like this:

typedef struct {
  enum {
    TYPE_DOUBLE,
    TYPE_INT,
    TYPE_STRING,
    TYPE_OBJECT,
    TYPE_BOOLEAN_TRUE,
    TYPE_BOOLEAN_FALSE,
    TYPE_NULL
  } type;

  int32_t as_int;
  double as_double;
  void* as_object;
  char* as_string;
} value;

Notice that I have also changed the order of as_int and as_double. Without that, my compiler still used to push additional space inside for better alignment. Now, it is aligned 4 4 8 8 8, which is fairly well and gives overall size 32 bytes.

But…

…it is as much as 32 bytes! It looks like a real overdose for storing values with the longest one being just 8 bytes. Moreover, if we decide to add a new type in the future, the struct’s size will grow even more.

We need something better. We need tagged unions!

Tagged union

Let’s see the better version of our little big struct:

typedef struct {
  enum {
    TYPE_DOUBLE,
    TYPE_INT,
    TYPE_STRING,
    TYPE_OBJECT,
    TYPE_BOOLEAN,
    TYPE_NULL
  } type;

  union {
    double double_num;
    int32_t int_num;
    char* string_ptr;
    void* object_ptr;
    char boolean; //There is no bool type in old C
  } as;
  
} value;

If you are familiar with unions in C, you can skip this little paragraph. If not, here is a quick recap.

Unions

A union is a special value representation in C that allows storing some data in multiple formats in the same place in memory. It is a perfect solution for our problem, as it can store our value, no matter what it is exactly, without much care of its type. It just squeezes all possible types in one place in memory by overlapping them and such bits can be read as representing one of the member types.

Here is a little sketch of this union:

union {
  char foo;
  int bar;
};

We have 4 bytes for int and 1 byte for char. In memory, these two types overlap each other. In other words, these bytes can be interpreted as char or as int.

Unions have always the size of their biggest member. In this case, the union is 4 bytes long, as int is of the longest one type inside.

Getting back to our code

So, by using union, our code for setting and getting values changes a little:

value foo;

foo.type = TYPE_INT;
foo.as.int_num = 123;

if(foo.type == TYPE_STRING){
  printf("string %s\n", foo.as.string_ptr);
}

However, it is still pretty straightforward and fast. The greatest advantage over the previous bad version is reduced struct’s size. Now, it is just the enum, which is 4 bytes long, and union, which has the longest type (double, or pointers) of 8 bytes, which overall gives us 12 bytes. It can be optimized further by choosing char instead of enum to 9 bytes. Either way, compilers probably align the struct to 16 bytes.

That is much better than the previous 48 or even 32 bytes. Actually, such an implementation is useful for simulating dynamic types in statically-typed languages like C/C++.

But our problem of storing and accessing types resolved at runtime still looks quite inefficiently. From 25% to almost half of the struct’s memory is allocated in vain. 16 bytes means that on the 64-bit machine two writes are required to load the value into CPU’s registers.

So, two obvious improvements can come to mind:

1. Compression of the union — if it is shorter than 8 bytes, it would be possible to fit everything in 8 bytes.
2. Removal of the type tag — it gives the dangling byte, so if we can get rid of it or cram it somewhere, the struct will be 8 bytes long as well.

The first option seems to be impossible with our condition that we would like to store double directly. This type just has to have all the 64 bits present. The same situation is for… pointers?

We can cut off a pretty significant part of a pointer’s bits actually, without losing any of its meaning. Read carefully and you will see!

Let’s begin making things a little crazy

Just for a moment assume that we do not have to pack double inside our structure. Instead of this, let’s use double* pointing to the actual value of this number. As we saw, double was the problematic union’s member, so now things should go easier, shouldn’t they? But do not worry about the double, we will restore it later, I promise!

What if our struct looked like this?

typedef union {
  uint64_t as_uint64;
  void* as_object_ptr;
} value;

Well, it is not a struct anymore, just a union now. It has 8 bytes, but what happened with all the fields we used to have? What happened with the tag? How to recognize what type it represents? Why did we introduce some unsigned int of 64-bit size? It is not obvious. Or it was not for me when I saw it for the first time.

Padding again

Do you remember the struct alignment mentioned in some paragraphs above? There — it hurts a little, here it helps.

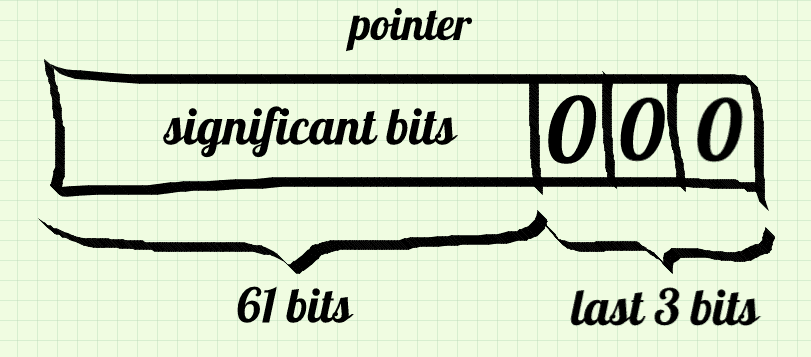
Not only do compilers try to align everything to some multiple of 8, but memory allocator does the same as well. It means that it is pretty sure that whether you allocate some memory at the heap, you will get a pointer which address is divisible by 8, especially when you want to allocate chunks of 8 bytes, like our good old struct value (or union now).

The advantage is that the last 3 bits of every pointer from malloc should be zeros. Actually, I suppose there is no guarantee about that, but in reality, all allocators do so. For example, GNU libc malloc, even on 32-bit platforms, aligns addresses to multiples of 8.

These three bits are the place where the tag, missing at the first glance in this union, is moved. They give us 8 possible values, which are enough for our needs about a few types. But this approach will not let us store and read values as directly as before. We will need to use some bitmasks.

Jugling bits is what tigers like best!

This is how a typical 64-bit pointer looks like:

It means that we can treat all our values as e.g. void * pointers when the last three bits are 000. With a little help from macros, we can dereference and set such pointers directly:

#define IS_OBJECT_PTR(v) ((v.as_uint64 & 7) == 0)

value foo;
void* bar; //Some pointer to object

//Setting value as an object pointer (even easier than before!)
foo->as_object_ptr = bar;

//Reading as object's pointer
if(IS_OBJECT_PTR(foo)){
  printf("It's an object with address %p\n", foo->as_object_ptr);
}

Not so bad, isn’t it?

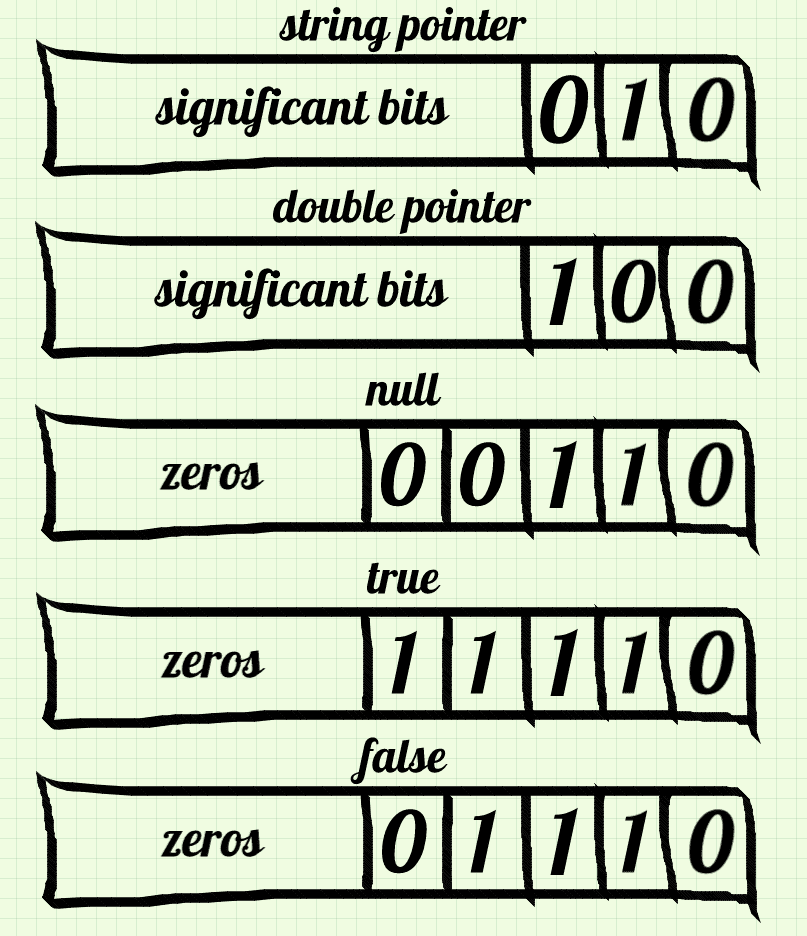
Let’s pack other types! Now, it is completely our decision which bit patterns represent which type, so I will go for this way:

You might have noticed that I have not mentioned the integer type. It can work kind of differently:

Everything that has 1 at the end is treated as an integer. It might seem like a waste of our precious 3 bits to use 1 of them just for encoding one type. However, it is not me who invented such an approach. But before I explain it, let’s see some code for dealing with these crazy patterns.

#define NULL_VALUE 0x6
#define TRUE_VALUE 0x1E
#define FALSE_VALUE 0x0E

#define IS_OBJECT_PTR(v) ((v.as_uint64 & 0x7) == 0x0)
#define IS_STRING_PTR(v) ((v.as_uint64 & 0x7) == 0x2)
#define IS_DOUBLE_PTR(v) ((v.as_uint64 & 0x7) == 0x4)
#define IS_NULL(v) (v.as_uint64 == NULL_VALUE)
#define IS_BOOL(v) ((v.as_uint64 & 0xF) == 0xE)
#define IS_INT(v) (v.as_uint64 & 0x1)

#define GET_AS_OBJECT_PTR(v) (v.as_object_ptr)
#define GET_AS_STRING_PTR(v) ((char*)(v.as_uint64 ^ 0x2))
#define GET_AS_DOUBLE_PTR(v) ((double*)(v.as_uint64 ^ 0x4))
#define GET_AS_BOOL(v) ((char)(v.as_uint64 >> 4))
#define GET_AS_INT(v) ((int32_t)(v.as_uint64 >> 1))

#define MAKE_OBJECT_PTR(p) ((uint64_t)(p))
#define MAKE_STRING_PTR(p) ((uint64_t)(p) | 0x2)
#define MAKE_DOUBLE_PTR(p) ((uint64_t)(p) | 0x4)
#define MAKE_INT(i) (((uint64_t)(i) << 1) | 0x1)

//Let's use those macros

value foo;
char* some_string;

// Setting

foo.as_uint64 = MAKE_STRING_PTR(some_string);
foo.as_uint64 = MAKE_INT(234);
foo.as_uint64 = FALSE_VALUE; //boolean

// Reading

if(IS_STRING_PTR(foo)){
  printf("string: %s\n", GET_AS_STRING_PTR(foo));
}
else if(IS_INT(foo)){
  printf("int: %d\n", GET_AS_INT(foo));
}
else if(IS_BOOL(foo)){
  printf("bool: %s\n", GET_AS_BOOL(foo) ? "true" : "false");
}

Lots of macros, but using all the types is still pretty simple.

Who is using this?

This way of squeezing many types into a pointer is a method called tagged pointers. I suppose it is a pretty old trick, but surprisingly, it is still widely used.

One of JavaScript’s implementations, Google’s V8 engine, actually uses tagged pointers for dynamic typing. Moreover, it uses the same way of storing integers as above!

Wait, integers in JavaScript? This language supports only doubles, so why do they store integers as an additional type? Well, integers are faster than doubles and in many cases, in JavaScript, we actually use integers, for example in loops:

for(let i = 0; i < someArray.length; i++){
  //do something
}

If the engine uses integers under the hood instead of doubles, such loops become a little faster.

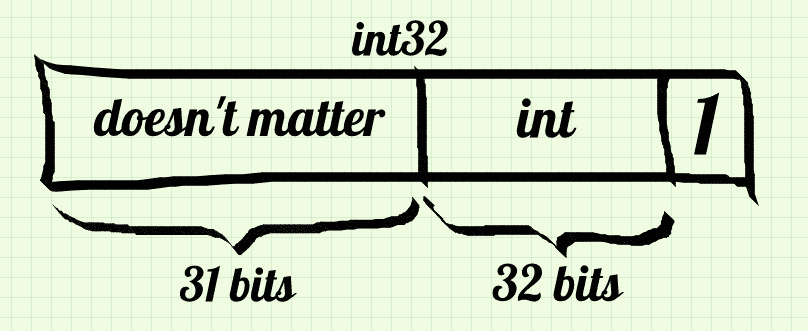
Okay, they have integers, but why do they use only one bit for recognizing them? One of the reasons might be the backward compatibility with 32-bit architectures. As with 64-bit pointers, you can store a full 32-bit integer, in a 32-bit pointer, you cannot cram it fully without ambiguity. So they decided that on 32-bit platforms they store 31-bit “small integers”, called ”Smis”. The 32nd bit is for recognizing them from pointers. The same approach was followed above in my code.

Pros and cons

Tagged pointers are actually used. It means that they are fairly good. Actually, they take only 8 bytes on 64-bit machines or even 4 bytes on 32-bit ones. Reading and storing data, when we have those macros defined above, is still pretty easy and fast, as processing units are very keen on bitwise operations. Moreover, there is still a chance that our macros can be optimized by compilers for specific platforms. Finally, they are pretty portable — allocators tend to behave gracefully and align memory cells to multiples of 8.

One of the disadvantages of tagged pointers is that they can store only a few different types, e.g. only 8 types of pointers with straightforward casting. They might also seem quite complicated and require those macros to make things easier. There are some views that problems with null pointers can occur, but without storing actual nullptr everything should work.

But the biggest problem from our perspective (do you remember our goal here?) is that storing doubles directly seems impossible. Fortunately, probably many decades ago, some powerful engineers invented another way of packing types called NaN boxing…

… and this is the real genius!

Okay, let’s change our value struct/union again.

typedef union {
  uint64_t as_uint64;
  double as_double;
} value;

Previously, we had a pointer, now we have double. The unsigned integer is still there, as it is useful for bitwise manipulations. It means that know we can read directly floating-point numbers. But how can we get pointers from such a union? You will see in a moment.

Quick recap about floating-point numbers.

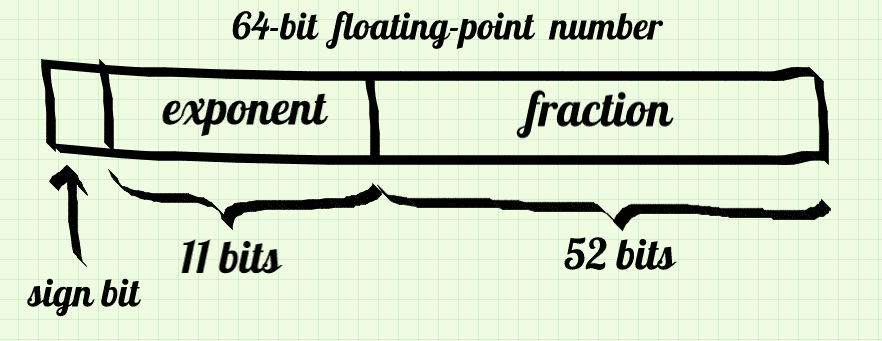
They allow us to store a great range of numbers with quite big precision and in our double case they occupy 64 bits. In this article, we do not care how they work actually, but it is vital to see how they are stored in memory:

There is one bit that says whether the number is negative or positive, 11 bits for exponent and 52 bits of the fraction part, also called mantissa.

No matter how it all works, we need to learn one more thing. There is a special value called NaN (Not a Number), which is yielded as a result of some illegal computations (like 0/0 or square of a negative number). We can see how it looks:

#include<math.h>
//...
value bar;
bar.as_double = NAN;

printf("%lx", barr.as_uint64); //7ff8000000000000

Fortunately or not, there is more than one NaN. IEEE 754 standard says that every floating-point value with all the exponent bits filled with 1 and at least one fraction bit as 1 (in order to distinguish from infinity) is NaN. It says that the remaining 51 bits (or 52 if sign bit counts) do not actually matter. They are called payload and can serve as a place for storing some information about the reason for NaN.

Let’s hide something inside

I suppose you have already guessed what we are going to do with them. Those remaining bits of NaN can be a place for storing our data, however, one might wonder if those bits may be filled somehow in NaNs yielded by arithmetic operations. The answer is “they should not be filled”. Every modern computer architecture leaves them as zeros. Moreover, probably every computer also sets the first bit of fraction to 1 when it is a NaN (if you are interested, read about quiet and signaling NaN). Thanks to this fact we can distinguish an actual NaN (always 7ff8000000000000) from our own NaN-ish value which is still useful for us after some bitwise manipulation.

Okay, the first step is to distinguish non-NaN doubles and the real NaN from our secret NaNs.

The first bit in the mantissa is a flag that says “it is kind of NaN”. The second bit means “it is our NaN, no the usual one”. Doing so wastes one bit of our precious memory, however, it makes type checking easier than if we checked presents of any bit “outside” the normal NaN.

#define NANISH 0x7ffc000000000000

#define IS_DOUBLE(v) ((v.as_uint64 & NANISH) != NANISH)

#define GET_AS_DOUBLE(v) (v.as_double)

How does it work?

1. If v is the real NaN, the left side is equal to the real NaN, which is different from our NaN-ish.
2. If v is a valid number, at least one of the exponent bits is zero, which makes it different from any NaN.
3. If v is kind of boxed value, the only difference from NaN-ish is outside the mask, so it gives us the NaN-ish mask.

It is pretty complicated, isn’t it? But still, it is fast and efficient, and with other types, everything will be a little easier now.

Simple values

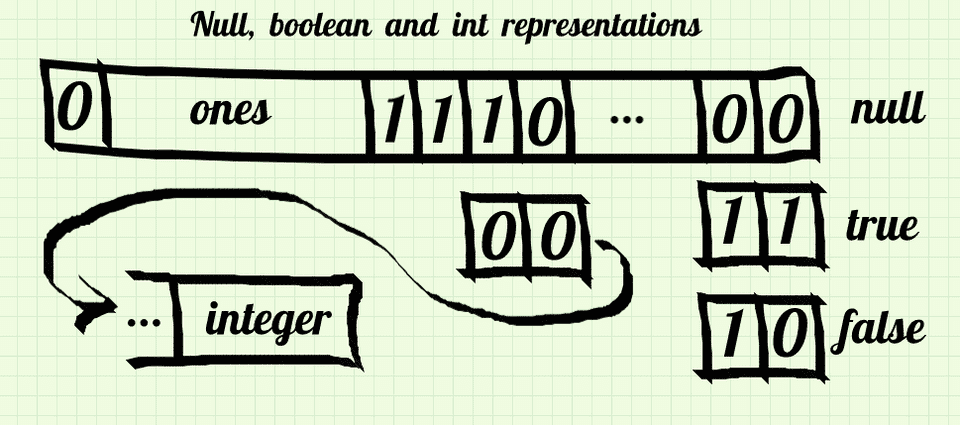
The time has come for null, booleans and integers. They will have a pretty straightforward representation. We are going to use the third bit of a fraction part and the last two bits. Third bit as 1 will mean “it is boolean or null”, as 0 “it is an integer”. The actual value will be encoded at the end of the fraction part, like this:

And the mighty code for this:

#define NANISH_MASK 0xffff000000000000
#define BOOLEAN_MASK 0x7ffe000000000002
#define INTEGER_MASK 0x7ffc000000000000

#define TRUE_VALUE (BOOLEAN_MASK | 3)
#define FALSE_VALUE (BOOLEAN_MASK | 2)
#define NULL_VALUE 0x7ffe000000000000

#define IS_NULL(v) (v.as_uint64 == NULL_VALUE)
#define IS_BOOL(v) ((v.as_uint64 & BOOLEAN_MASK) == BOOLEAN_MASK)
#define IS_INT(v) ((v.as_uint64 & NANISH_MASK) == INTEGER_MASK)

#define GET_AS_BOOL(v) ((char)(v.as_uint64 & 0x1))
#define GET_AS_INT(v) ((int32_t)(v.as_uint64))

Pointers

Okay, now pointers. But as far as we know, on 64-bit architectures pointers have 64 bits and our tricks with NaN can hold only around 52 bits. If we can cut off some insignificant pointer’s bits… Yes, I told that the last 3 bits tend to be zeros, but that is still not enough. But there is another issue worth observing.

64 bits gives us a huge amount of memory addresses. So huge, that most of them are not necessary with today’s memory capacities. Because of that, 64-bit architectures use only 48 lowest bits of every pointer which still give plenty of addresses. It means that only 48 bits in a pointer are significant and that is enough for our NaN boxing. What about the rest? It’s quite strange, but on most popular systems they should be zeros. There are some problems with systems like e.g. Solaris, but it is still possible to fix them somehow and it is out of scope of this little article.

In our implementation, we can store pointers in the last 48 bits of our union. The sign bit can indicate that it is some kind of pointer, and first free bits of fraction part can decide about its real type, like this:

#define OBJECT_MASK 0xfffc000000000000
#define STRING_MASK 0xfffe000000000000

#define IS_OBJECT_PTR(v) ((v.uint64_t & NANISH_MASK) == OBJECT_MASK)
#define IS_STRING_PTR(v) ((v.uint64_t & NANISH_MASK) == STRING_MASK)

#define GET_AS_OBJECT_PTR(v) ((void*)(v.as_uint64 & 0xFFFFFFFFFFFF))
#define GET_AS_STRING_PTR(v) ((char*)(v.as_uint64 & 0xFFFFFFFFFFFF))

Setters

The last things we need to do are setter macros. We do not need such a macro for double, however, adding it could be useful if we wished to make all setter uniformly. But I will not do so here. This article is long enough now :)

#define MAKE_OBJECT_PTR(p) ((uint64_t)(p) | OBJECT_MASK)
#define MAKE_STRING_PTR(p) ((uint64_t)(p) | STRING_MASK)
#define MAKE_INT(i) ((uint64_t)(i) | INTEGER_MASK)

Fairly easy, isn’t it? And we are done!

Is it madness?

NaN boxing seems really crazy. Almost every possible combination of those 64 bits can store some valid value, we juggle with all those masks and bits. But is it very useful? Yes.

This peculiar technique is used by LuaJIT, Mozilla’s JavaScriptCore and some other dynamically-typed languages implementations.

Upsides of NaN boxing

1. It is memory-efficient, especially on 64-bit architectures, using a minimal amount of memory for those types — 8 bytes.
2. Unlike tagged pointers, it allows storing 64-bit floating-point numbers. There is no need for storing them on the heap and passing by pointers — which can be expensive.
3. It seems like as fast option as tagged pointers (we will check that in a moment).

Downsides

1. It is complicated, you see.
2. On 32-bit computers it is still some waste of memory — tagged pointers use only 4 bytes.
3. It is based on many quite blurry assumptions about memory allocators, floating-point arithmetics, pointers’ sizes, etc., which might not be true for some platforms and not be future-proof.

For example, I did a little research in order to ask the question: why did not V8 go for it? It seems like there is no one special reason for that, but many. Firstly, the second point of downsides — memory waste on 32 bits, which can be crucial for some devices. Secondly, they have tagged pointers, which is still a good option. Finally, they are said to have decent memory management with the doubles on the heap.

Make pointers fast again

Actually, while implementing NaN boxing, we can take one of two approaches. We can prefer doubles or pointers. In the implementation above, we chose to treat the union by deault as doubles, so getting their values does not require any bitwise operations and is faster. But with more bitpain we could store pointers directly, and shift and mask our union to get double value, which could be helpful if we would like to dereference pointers quickly. I suppose it is a matter of taste here. SpiderMonkey favors doubles, Webkit is pointer-friendly.

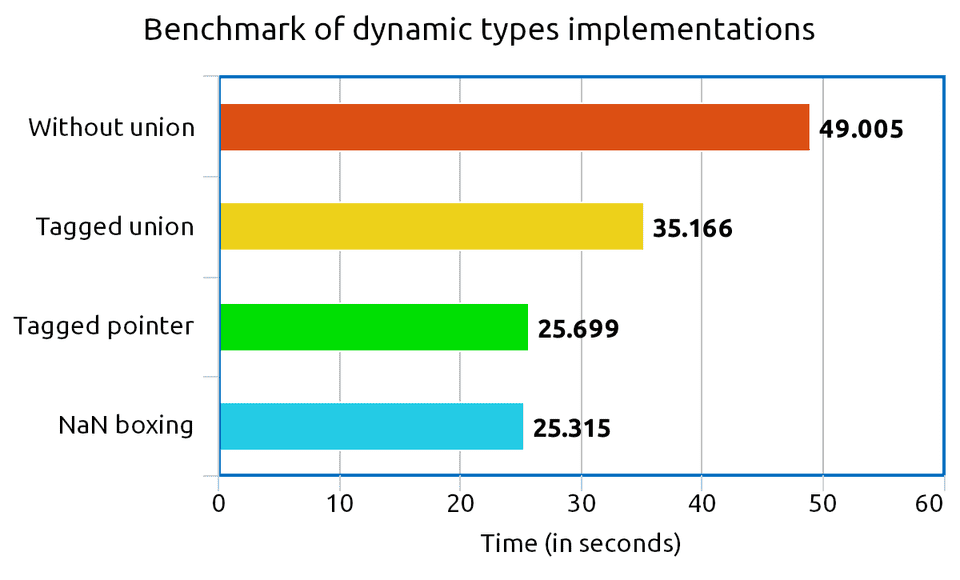
Benchmark

I decided to check if there is a real difference between all those representations of dynamic types, so I prepared some time tests. Here you can download them if you wish.

The benchmark allocates many of our value representations, and then it stores, checks, and reads random types and data in a big loop, 500.000.000 times. The results I obtained are not so surprising:

Conclusion: struct size matters. The smaller our structure is, the faster it can be loaded into CPU registers and everything should work more efficiently.

I noticed that there is little performance difference between tagged pointers and NaN boxing. Actually, they have the same memory print and similar techniques for assignments and reads. This might be another reason why both these solutions are popular in e.g. JavaScript implementations.

Summary

When I noticed the NaN boxing method for the first time in Robert Nystrom’s book Crafting Interpreters, it really surprised me. It is so tricky, but as a great admirer of tiny optimizations, I consider it beautiful as well.

However, there is little information about it around the web despite its popularity among language hackers. It is always great to discover such tricks and to test them, as the knowledge of how things work under the hood makes you always be a little better programmer, writing a little more efficient things.